Teorema do número primo: a relação de e^x com os números primos

Teorema do número primo

Este estudo busca mostrar a relação aparentemente implícita de e^x para a distribuição dos números primos. Foi formulada pelo autor Nickson Grimes durante uma análise da fórmula proposta por Carl Friedrich Gauss a respeito da distribuição dos números primos.

Teorema do número primo

O teorema do número primo \(\frac {n} {ln(n)} = p\) mostra a relação da distribuição de primos através da natureza do logaritmo natural que é capaz de prever a quantidade de números primos dado uma quantidade de números que se insere na equação. Conforme a quantia aumente, mais precisa se torna a aproximação.

Partindo do teorema:

Se \(\frac {n} {ln(n)} = p\) , onde N é uma quantidade de números de interesse, e P é a quantidade de números primos existentes até esse valor, onde \(\frac {p} {n} = \%\) ou densidade de números primos, então podemos fazer o seguinte:

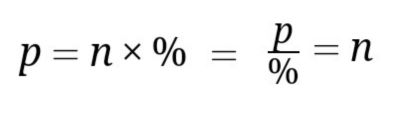
Vamos usar uma densidade de 1%, logo:

Substituindo em \(\frac {n} {ln(n)} = p\), logo:

Note que essa é apenas a quantidade de números para uma densidade 1%. Se fizermos \(p = n \times \%\), teremos a quantidade de primos:

Isso pode ser provado pelo próprio teorema do número primo:

E note que:

Bibliografia

Khan academy (canal) YouTube: https://youtu.be/AQTIa02NNZ0?si=tQ0rGDa1tHnlCGye

Toda a matemática (canal) YouTube: https://youtu.be/wIbufxcWpPI?si=iy-Swhi9aMC7bfqr

Toda a matemática (canal) YouTube: https://youtu.be/calR7_x-BGE?si=bzzwdSpK3qBxrTYk