Porquê que na lei dos cossenos a fórmula usada é negativa e na regra do paralelogramo ela fica com o sinal positivo?

Primeiramente, a lei dos cossenos é usada quando temos um triangulo que nus forneça o valor de um ângulo e dois lados, consequentemente sabemos determinar o lado que está em frente ao ângulo.

Assim para sabermos o tamanho do lado R usamos a lei dos cossenos: R² = B² + A² – 2* A* B * Cos (α).

Agora depois dessa visualização podemos dar uma olhada na regra do paralelogramo:

Usamos essa regra do paralelogramo quando temos dois vetores é um ângulo formado entre eles.  Para determinar o vetor resultante dessa soma vetorial, usamos à lei dos cossenos com o sinal de mais: R² = B² + A² + 2* A* B * Cos (θ).

Com base nesses dois comentários: Por qual razão um si usa positivo e outro negativo na formula?

Não é esse o ponto si um usa positivo ou negativo, mas sim o ângulo que usamos para fator de cálculo. Vou demostrar como que ocorre essa escolha dos ângulos. Para isso devemos pensar primeiramente no principal da lei dos cossenos que é utilizada com um triangulo e si usarmos esse pensamento podemos pensar na regra do poligonal.

No método do poligonal um vetor e colocado a sua origem na extremidade do outro e pode ser feito com vários vetores (aqui iremos usar esse pensamento para identificarmos a razão do sinal que está diretamente relacionado ao ângulo). Como eu disse a lei dos cossenos e usada né um triângulo, e logo quando temos dois vetores e traçar o vetor resultante veremos uma formação de um triângulo e com um ângulo entre eles. Assim a imagem mostra:

Note para achar o vetor resultante teríamos que colocar a origem dele na origem do vetor B e com sua extremidade na extremidade do vetor A. Como pode perceber o ângulo dele e alfa que conseguintemente podemos usar a lei dos cossenos original, mas só estamos usando à lei dos cossenos original aqui porquê formou um triangulo e por fins didáticos formou o mesmo ângulo e que é da primeira figura.

O módulo do vetor resultante R pode ser encontrado por: R² = B² + A² – 2* A* B* Cos(α).

Como pode perceber si mudarmos alfa (α) para teta (θ) mudamos o sinal de negativo para positivo. Mas podem surgir muitas dúvidas. Como porque usamos a regra do paralelogramo? Porque na maioria dos casos os vetores têm sua origem no mesmo lugar, perceba por exemplo aceleração, força peso e outras que quando são decompostas em planos horizontal e vertical ficam com suas origens no mesmo ponto. Outra dúvida pode ser porque usamos a regra do poligonal? Essa por sua vez e usado em casos que temos dois ou mais vetores e que estão no papel quadriculado, pois, mais fácil para si determinar o modulo do vetor resultante.

Com base nisso teta e alfa tem uma relação qual é?

Para entender essa relação iremos buscar na geometria na parte de retas paralelas cortadas por uma transversal.

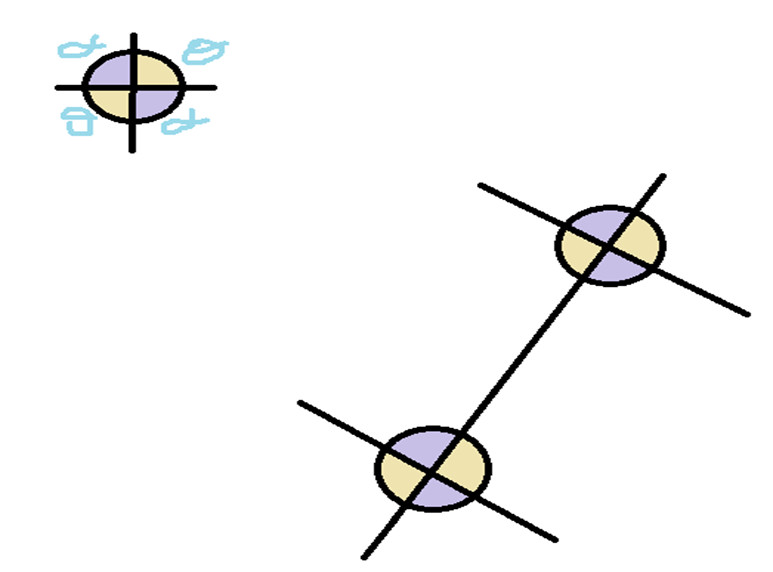
Note que a cor mais clara é a formação do ângulo teta (θ) e a cor mais escura é a formação do ângulo alfa (α). Assim percebemos a relação principal que teta mais alfa e igual a cento e oitenta graus: α + θ = 180º.

Agora com base nessa visualização podemos colocar os vetores A e B nessa reta.

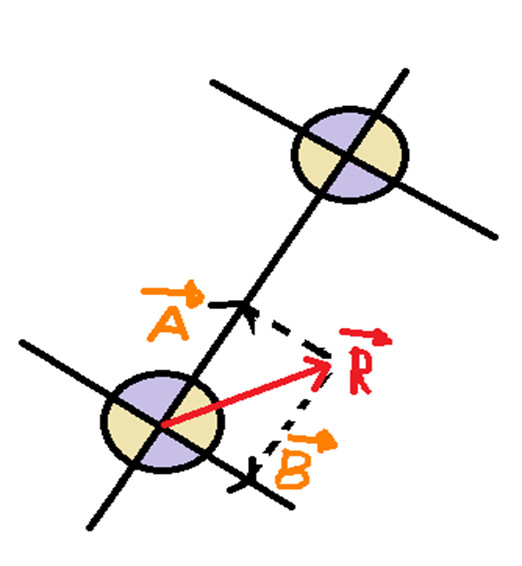
Com base nesse desenho notamos que o ângulo formado entre o vetor A e B e teta, quero que vocês percebam que si eu colocar de modo que fosse a regra do poligonal, poderíamos trasladar com o vetor B e colocar como diz a regra e iriamos visualizar que o ângulo formado seria consequentemente alfa:

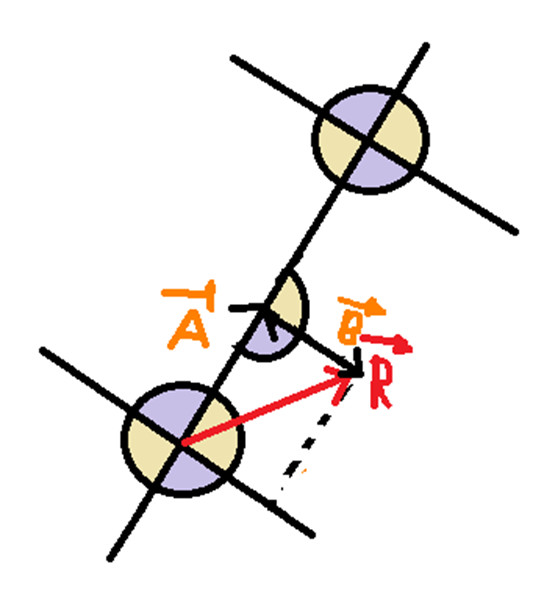
Com base com colocamos para fins didático o ângulo formado entre o vetor A e B seria o alfa.

Mas lembrando que eu disse α + θ = 180º podemos levar inconsideração que 180° - θ = α. Pois, podemos pegar a formula original que é:

• R² = B² + A² – 2* A* B * Cos (α). Mas como estamos precisando usar teta (θ), pois queremos usar a regra do paralelogramo, assim, podemos usar 180° - θ = α. Perceba que posso tirar α e colocar 180° - θ, pois, a equação diz que quando temos o sinal de igual é porquê os dois lados são iguais.
• R² = B² + A² – 2* A* B * Cos (180° - θ). Mas si vocês colocarem na subtração de arcos cos (180° - θ) iram identificar que a resposta é – cos (θ).
• R² = B² + A² – 2* A* B * (-Cos (θ)). Logo o menos está multiplicando o menos da formula e ficamos com o mais.
• R² = B² + A² + 2* A* B * Cos (θ). Portanto essa é a formula da regra do paralelogramo.

Mas para deixar bem esclarecido temos que:

Para saber que Cos (180° - θ) = -cos (θ). Temos que usar a subtração de arcos que é cos (a – b) = sen(a) * sen(b) + cos(a) * cos(b). Colocando os valores que queremos temos:

•cos (180°- θ) = sen (180°) * sen (θ) + cos (180°) * cos (θ)

•cos (180°- θ) = 0 * sen (θ) + (-1) * cos (θ) 

•cos (180°- θ) = -cos (θ)

Agora para finalizar temos a subtração de vetores no método paralelogramo.

Quando queremos subtrair vetores fazemos o seguinte. Exemplo vetor A menos o vetor B: A-B = R, que R é o vetor resultante da subtração nesse caso.

Com base no nosso raciocino temos:

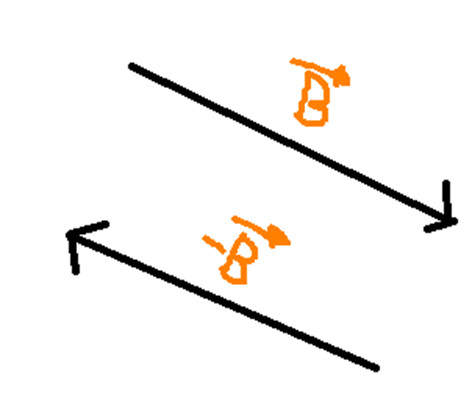
Percebemos que quando temos uma representação do vetor –B temos o sentido oposto. Agora vamos colocar nas retas paralelas cortadas por uma transversal:

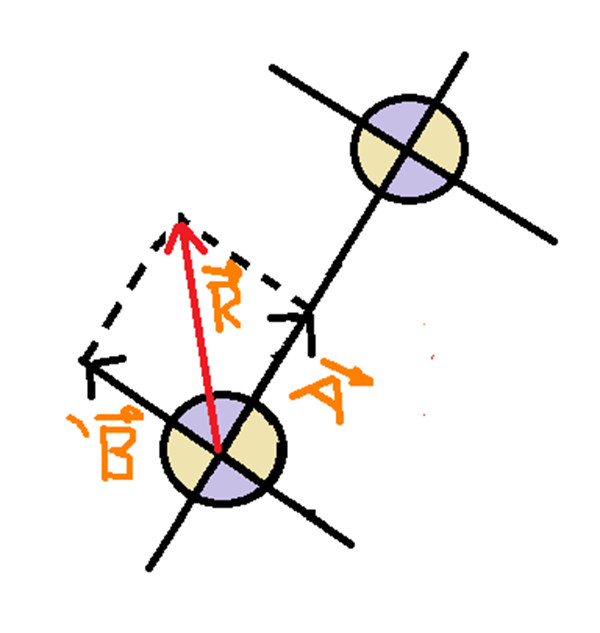
Com base que vimos o ângulo formado nessa cor mais escura e o alfa (α), logo na subtração de vetores temos a formula idêntica a lei dos cossenos porque o sentido do vetor B mudou logo o ângulo mudou. É também fica valido que para achar o modulo do vetor resultante (R): R² = B² + A² – 2* A* B * Cos (α).

Percebam que não muda o sinal é sim o ângulo estudado!